

Next: DFA-1 on linear trend
Up: Appendix
Previous: Noise
Superposition law for DFA
For two uncorrelated signals 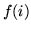 and
and 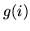 , their root mean
square fluctuation functions are
, their root mean
square fluctuation functions are 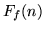 and
and 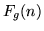 respectively. We want to prove that for the signal
respectively. We want to prove that for the signal
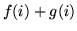 , its rms fluctuation
, its rms fluctuation
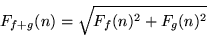 |
(27) |
Consider three signals in the same box first. The integrated signals for 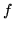 ,
, 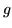 and
and 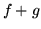 are
are 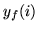 ,
, 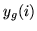 and
and 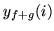 and their corresponding trends are
and their corresponding trends are 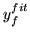 ,
, 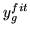 ,
,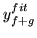 (
(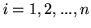 ,
, 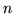 is the box size).
Since
is the box size).
Since
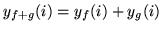 and combine the definition of detrended fluctuation function Eq.3, we have that for all boxes
and combine the definition of detrended fluctuation function Eq.3, we have that for all boxes
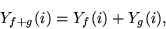 |
(28) |
where 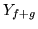 is the detrended fluctuation function for the
signal
is the detrended fluctuation function for the
signal 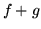 ,
, 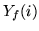 is for the signal
is for the signal 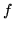 and
and 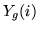 for
for 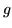 . Furthermore, according to the definition of rms
fluctuation, we can obtain
. Furthermore, according to the definition of rms
fluctuation, we can obtain
![\begin{displaymath}
F_{f+g}(n) = \sqrt{\frac{1}{N_{max}} \sum\limits_{i=1}^{N_{...
...m\limits_{i=1}^{N_{max}}\left[Y_{f}(i)+Y_{g}(i)\right ]^2},
\end{displaymath}](img413.png) |
(29) |
where 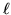 is the number of boxes and
is the number of boxes and 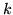 means the
means the 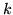 th box.
If
th box.
If 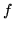 and
and 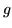 are not correlated, neither are
are not correlated, neither are 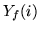 and
and 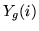 and, thus,
and, thus,
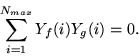 |
(30) |
From Eq.30 and Eq.29, we have
![\begin{displaymath}
F_{f+g}(n)=\sqrt{\frac{1}{N_{max}} \sum\limits_{i=1}^{N_{ma...
...}
=\sqrt{\left[F_{f}(n)\right ]^2+\left[F_{g}(n)\right ]^2}.
\end{displaymath}](img417.png) |
(31) |


Next: DFA-1 on linear trend
Up: Appendix
Previous: Noise
Zhi Chen
2002-08-28
![\begin{displaymath}
F_{f+g}(n)=\sqrt{\frac{1}{N_{max}} \sum\limits_{i=1}^{N_{ma...
...}
=\sqrt{\left[F_{f}(n)\right ]^2+\left[F_{g}(n)\right ]^2}.
\end{displaymath}](img417.png)