


Next: Bibliography
Up: manual
Previous: A Research Example
Other Models
In addition to the models of Section 2, other lumped
parameter models of the pulsatile heart and circulation and resting
physiologic perturbation models may be implemented with the RCVSIM source code. These models may only be implemented at the
MATLAB prompt by executing simulate.mexlx. A brief description
of each of these models and the relevant MATLAB functions is given
below.
- Lumped parameter models of the pulsatile heart and circulation
- Left ventricle preparation. The electrical circuit analog
of this preparation may be visualized by replacing
 and
and
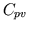 in Figure 1 with the DC voltage sources
in Figure 1 with the DC voltage sources
 and
and 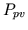 , respectively. This preparation may be utilized
for the analysis of the input-output properties of the left
ventricle model; however, there is currently no source code to alter
the DC voltage sources during a single simulation. The
initial pressure, volume, and flow rate of the preparation are
computed with the function lv_init_cond.m, and the
derivative of the pressure at a desired time step is determined with
the function lv_eval_deriv.m.
, respectively. This preparation may be utilized
for the analysis of the input-output properties of the left
ventricle model; however, there is currently no source code to alter
the DC voltage sources during a single simulation. The
initial pressure, volume, and flow rate of the preparation are
computed with the function lv_init_cond.m, and the
derivative of the pressure at a desired time step is determined with
the function lv_eval_deriv.m.
- Intact circulatory preparation for measurement of single
ventricular contraction
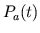 response. The electrical
circuit analog of this preparation is given by
Figure 1and includes an additional parameter (
response. The electrical
circuit analog of this preparation is given by
Figure 1and includes an additional parameter (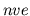 )
which represents the beat number after which the ventricles will no
longer contract. The single ventricular contraction
)
which represents the beat number after which the ventricles will no
longer contract. The single ventricular contraction 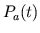 response may then be determined by executing the preparation for
response may then be determined by executing the preparation for
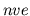 , and then
, and then 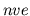 -1, ventricular contractions and then taking
the difference between the two resulting
-1, ventricular contractions and then taking
the difference between the two resulting 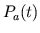 waveforms.
waveforms.
- Intact circulatory preparation with only linear elements.
The electrical circuit analog of this preparation is given by
Figure 1 in which the four nonlinear elements are
replaced by purely linear elements. This model was previously
presented by Davis [3]. The initial pressures,
volumes, and flow rates of the preparation are computed with the
function init_cond.m, and the derivative of the pressures at
a desired time step is determined with the function eval_deriv.m.
- Intact circulatory preparation with third-order systemic
arteries. The electrical circuit analog of this preparation may
be visualized by replacing the capacitor
 in
Figure 1 with two grounded capacitors connected via
an inductor. The capacitor proximal to the left ventricle
compartment represents the large, elastic (
in
Figure 1 with two grounded capacitors connected via
an inductor. The capacitor proximal to the left ventricle
compartment represents the large, elastic (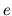 ) arteries, the other
capacitor represents the small, muscular (
) arteries, the other
capacitor represents the small, muscular (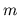 ) arteries, and the
inductor (
) arteries, and the
inductor (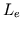 ) accounts for the inertial effects of blood flow
between the two lumped arteries. This third-order model of the
systemic arteries was previously presented by Clark
[2]. The
) accounts for the inertial effects of blood flow
between the two lumped arteries. This third-order model of the
systemic arteries was previously presented by Clark
[2]. The 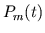 waveform may be considered as a
first-order approximation of a peripheral arterial blood pressure
waveform. The initial pressures, volumes, and flow rates of the
preparation are computed with the function third_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function third_eval_deriv.m.
waveform may be considered as a
first-order approximation of a peripheral arterial blood pressure
waveform. The initial pressures, volumes, and flow rates of the
preparation are computed with the function third_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function third_eval_deriv.m.
- Intact circulatory preparation with nonlinear systemic
arterial compliance. The electrical circuit analog of this
preparation is given by Figure 1 with a box
encompassing
 to denote its nonlinearity. This nonlinear
element is characterized by the curvature (
to denote its nonlinearity. This nonlinear
element is characterized by the curvature ( ), differential
compliance (
), differential
compliance ( ), and volume (
), and volume (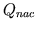 ) all at
) all at 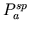 .
Provided that
.
Provided that  , the differential compliance decreases with
increasing
, the differential compliance decreases with
increasing 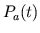 . The initial pressures, volumes, and flow rates
of the preparation are computed with the function nac_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function nac_eval_deriv.m.
. The initial pressures, volumes, and flow rates
of the preparation are computed with the function nac_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function nac_eval_deriv.m.
- Intact circulatory preparation with third-order systemic
arteries and nonlinear, large elastic arterial compliance. This
preparation is a combination of the previous two preparations with a
nonlinear
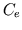 and linear
and linear  . The initial pressured, volumes,
and flow rates of the preparation are computed with the function
third_nac_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function third_nac_eval_deriv.m.
. The initial pressured, volumes,
and flow rates of the preparation are computed with the function
third_nac_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function third_nac_eval_deriv.m.
- Intact circulatory preparation with an arterial pressure
reservoir preparation. The electrical circuit analog of this
preparation may be visualized by replacing
 in
Figure 1 with a DC voltage source
in
Figure 1 with a DC voltage source  . This
preparation may be utilized to understand hemodynamics while
. This
preparation may be utilized to understand hemodynamics while
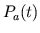 is held constant. The initial pressures, volumes, and flow
rates of the preparation are computed with the function apr_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function apr_eval_deriv.m.
is held constant. The initial pressures, volumes, and flow
rates of the preparation are computed with the function apr_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function apr_eval_deriv.m.
- Intact circulatory preparation with contracting atria.
The electrical circuit analog of this preparation may be visualized
by inserting right atrial (
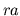 ) and left atrial (
) and left atrial (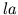 ) compartments
(linear resistor and linear, variable capacitor with an unstressed
volume) between the venous and ventricular compartments in
Figure 1. The atrial and ventricular compliances at
a desired time step are respectively computed by the functions var_vcap.m and var_acap.m. The initial pressures,
volumes, and flow rates of the preparation are computed with the
function a_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function a_eval_deriv.m.
) compartments
(linear resistor and linear, variable capacitor with an unstressed
volume) between the venous and ventricular compartments in
Figure 1. The atrial and ventricular compliances at
a desired time step are respectively computed by the functions var_vcap.m and var_acap.m. The initial pressures,
volumes, and flow rates of the preparation are computed with the
function a_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function a_eval_deriv.m.
- Resting physiologic perturbations
- Respiratory activity. In addition to fixed-rate breathing
and random-interval breathing with varying tidal volumes,
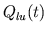 may also be represented as a step or impulse of desired
amplitude or area (Qfrs) and at a desired time (Qfrt) as
well as at random-intervals with a constant tidal volume.
These breathing patterns are generated with the function resp_act.m.
may also be represented as a step or impulse of desired
amplitude or area (Qfrs) and at a desired time (Qfrt) as
well as at random-intervals with a constant tidal volume.
These breathing patterns are generated with the function resp_act.m.
- Autoregulation of local vascular beds. In addition to
bandlimited white noise, autoregulation of local vascular beds may
also be represented as bandlimited, 1/f noise or a sinusoid of
desired amplitude (ar) and frequency (fr). The former
representation is generated with the functions bl_filt.m and
oneoverf_filt.m.
- Central oscillator. A central oscillator is represented
as an exogenous, sinusoidal disturbance to
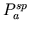 of desired
amplitude (ap) and frequency (fp).
of desired
amplitude (ap) and frequency (fp).
- Non-baroreflex mediated fluctuations in
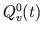 .
Fluctuations in
.
Fluctuations in 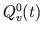 not due to the baroreflexes are
represented as a white disturbance of desired standard deviation
(stdwq) that is bandlimited to a desired frequency (
not due to the baroreflexes are
represented as a white disturbance of desired standard deviation
(stdwq) that is bandlimited to a desired frequency (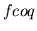 ).
These fluctuations may specifically be due to, for example, fast
acting hormonal loops. These fluctuations are generated with the
function bl_filt.m.
).
These fluctuations may specifically be due to, for example, fast
acting hormonal loops. These fluctuations are generated with the
function bl_filt.m.
In order to implement all of the above models, rather than using read_param.m, the parameter vector th must be created by
first copying the file $DIR/bin/header_def.m to the current
directory and then executing th=header_def; at the MATLAB
prompt (Note that header_def.m can be copied to any name as
long as it has the extension .m). Additionally, the appropriate
option of the arguments to simulate.mexlx (type help
simulate at the MATLAB prompt) must be selected.



Next: Bibliography
Up: manual
Previous: A Research Example
Ramakrishna Mukkamala (rama@egr.msu.edu)
2004-02-03
 and
and
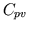 in Figure 1 with the DC voltage sources
in Figure 1 with the DC voltage sources
 and
and 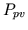 , respectively. This preparation may be utilized
for the analysis of the input-output properties of the left
ventricle model; however, there is currently no source code to alter
the DC voltage sources during a single simulation. The
initial pressure, volume, and flow rate of the preparation are
computed with the function lv_init_cond.m, and the
derivative of the pressure at a desired time step is determined with
the function lv_eval_deriv.m.
, respectively. This preparation may be utilized
for the analysis of the input-output properties of the left
ventricle model; however, there is currently no source code to alter
the DC voltage sources during a single simulation. The
initial pressure, volume, and flow rate of the preparation are
computed with the function lv_init_cond.m, and the
derivative of the pressure at a desired time step is determined with
the function lv_eval_deriv.m.
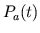 response. The electrical
circuit analog of this preparation is given by
Figure 1and includes an additional parameter (
response. The electrical
circuit analog of this preparation is given by
Figure 1and includes an additional parameter (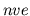 )
which represents the beat number after which the ventricles will no
longer contract. The single ventricular contraction
)
which represents the beat number after which the ventricles will no
longer contract. The single ventricular contraction 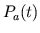 response may then be determined by executing the preparation for
response may then be determined by executing the preparation for
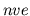 , and then
, and then 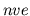 -1, ventricular contractions and then taking
the difference between the two resulting
-1, ventricular contractions and then taking
the difference between the two resulting 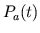 waveforms.
waveforms.
 in
Figure 1 with two grounded capacitors connected via
an inductor. The capacitor proximal to the left ventricle
compartment represents the large, elastic (
in
Figure 1 with two grounded capacitors connected via
an inductor. The capacitor proximal to the left ventricle
compartment represents the large, elastic (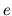 ) arteries, the other
capacitor represents the small, muscular (
) arteries, the other
capacitor represents the small, muscular (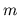 ) arteries, and the
inductor (
) arteries, and the
inductor (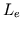 ) accounts for the inertial effects of blood flow
between the two lumped arteries. This third-order model of the
systemic arteries was previously presented by Clark
[2]. The
) accounts for the inertial effects of blood flow
between the two lumped arteries. This third-order model of the
systemic arteries was previously presented by Clark
[2]. The 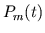 waveform may be considered as a
first-order approximation of a peripheral arterial blood pressure
waveform. The initial pressures, volumes, and flow rates of the
preparation are computed with the function third_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function third_eval_deriv.m.
waveform may be considered as a
first-order approximation of a peripheral arterial blood pressure
waveform. The initial pressures, volumes, and flow rates of the
preparation are computed with the function third_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function third_eval_deriv.m.
 to denote its nonlinearity. This nonlinear
element is characterized by the curvature (
to denote its nonlinearity. This nonlinear
element is characterized by the curvature ( ), differential
compliance (
), differential
compliance ( ), and volume (
), and volume (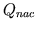 ) all at
) all at 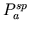 .
Provided that
.
Provided that  , the differential compliance decreases with
increasing
, the differential compliance decreases with
increasing 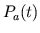 . The initial pressures, volumes, and flow rates
of the preparation are computed with the function nac_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function nac_eval_deriv.m.
. The initial pressures, volumes, and flow rates
of the preparation are computed with the function nac_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function nac_eval_deriv.m.
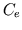 and linear
and linear  . The initial pressured, volumes,
and flow rates of the preparation are computed with the function
third_nac_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function third_nac_eval_deriv.m.
. The initial pressured, volumes,
and flow rates of the preparation are computed with the function
third_nac_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function third_nac_eval_deriv.m.
 in
Figure 1 with a DC voltage source
in
Figure 1 with a DC voltage source  . This
preparation may be utilized to understand hemodynamics while
. This
preparation may be utilized to understand hemodynamics while
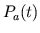 is held constant. The initial pressures, volumes, and flow
rates of the preparation are computed with the function apr_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function apr_eval_deriv.m.
is held constant. The initial pressures, volumes, and flow
rates of the preparation are computed with the function apr_init_cond.m, and the derivative of the pressures at a
desired time step is determined with the function apr_eval_deriv.m.
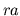 ) and left atrial (
) and left atrial (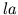 ) compartments
(linear resistor and linear, variable capacitor with an unstressed
volume) between the venous and ventricular compartments in
Figure 1. The atrial and ventricular compliances at
a desired time step are respectively computed by the functions var_vcap.m and var_acap.m. The initial pressures,
volumes, and flow rates of the preparation are computed with the
function a_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function a_eval_deriv.m.
) compartments
(linear resistor and linear, variable capacitor with an unstressed
volume) between the venous and ventricular compartments in
Figure 1. The atrial and ventricular compliances at
a desired time step are respectively computed by the functions var_vcap.m and var_acap.m. The initial pressures,
volumes, and flow rates of the preparation are computed with the
function a_init_cond.m, and the derivative of the pressures
at a desired time step is determined with the function a_eval_deriv.m.
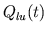 may also be represented as a step or impulse of desired
amplitude or area (Qfrs) and at a desired time (Qfrt) as
well as at random-intervals with a constant tidal volume.
These breathing patterns are generated with the function resp_act.m.
may also be represented as a step or impulse of desired
amplitude or area (Qfrs) and at a desired time (Qfrt) as
well as at random-intervals with a constant tidal volume.
These breathing patterns are generated with the function resp_act.m.
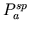 of desired
amplitude (ap) and frequency (fp).
of desired
amplitude (ap) and frequency (fp).
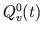 .
Fluctuations in
.
Fluctuations in 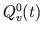 not due to the baroreflexes are
represented as a white disturbance of desired standard deviation
(stdwq) that is bandlimited to a desired frequency (
not due to the baroreflexes are
represented as a white disturbance of desired standard deviation
(stdwq) that is bandlimited to a desired frequency (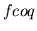 ).
These fluctuations may specifically be due to, for example, fast
acting hormonal loops. These fluctuations are generated with the
function bl_filt.m.
).
These fluctuations may specifically be due to, for example, fast
acting hormonal loops. These fluctuations are generated with the
function bl_filt.m.