

Next: Signals with segments removed
Up: Effect of nonstationarities on
Previous: Introduction
Method
Using a modified Fourier filtering method[63], we generate stationary
uncorrelated, correlated, and anti-correlated signals  (
(
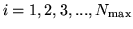 ) with a standard
deviation
) with a standard
deviation  . This method consists of the following steps:
. This method consists of the following steps:
(a) First, we generate an uncorrelated and Gaussian distributed sequence
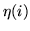 and calculate the Fourier transform coefficients
and calculate the Fourier transform coefficients 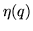 .
.
(b) The desired signal 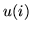 must exhibit correlations, which are
defined by the form of the power spectrum
must exhibit correlations, which are
defined by the form of the power spectrum
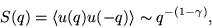 |
(1) |
where 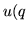 ) are the Fourier transform coefficients of
) are the Fourier transform coefficients of 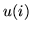 and
and 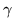 is the correlation exponent. Thus, we generate
is the correlation exponent. Thus, we generate 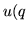 ) using the following
transformation:
) using the following
transformation:
![\begin{displaymath}
u(q)=[S(q)]^{1/2}\eta(q),
\end{displaymath}](img68.png) |
(2) |
where 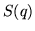 is the desired power spectrum in Eq. (1).
is the desired power spectrum in Eq. (1).
(c) We calculate the inverse Fourier transform of 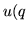 ) to obtain
) to obtain
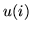 .
.
We use the stationary correlated signal 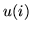 to generate signals with
different types of nonstationarity and apply the DFA method[3] to quantify
correlations in these nonstationary signals.
to generate signals with
different types of nonstationarity and apply the DFA method[3] to quantify
correlations in these nonstationary signals.
Next, we briefly introduce the DFA method, which involves the following
steps[3]:
(i) Starting with a correlated signal
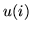 , where
, where
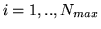 and
and 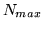 is the length of the signal,
we first integrate the signal
is the length of the signal,
we first integrate the signal 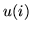 and obtain
and obtain
![$y(k)\equiv\sum_{i=1}^{k}[u(i)-\langle u \rangle]$](img72.png) , where
, where
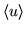 is the mean.
is the mean.
(ii) The integrated signal 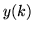 is divided into boxes of equal
length
is divided into boxes of equal
length 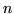 .
.
(iii) In each box of length 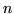 , we
fit
, we
fit 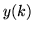 , using a polynomial function of order
, using a polynomial function of order 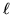 which represents the
trend in that box. The
which represents the
trend in that box. The 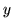 coordinate of the fit line in each box is denoted by
coordinate of the fit line in each box is denoted by 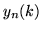 (see
Fig. 1, where linear fit is used). Since we use a polynomial
fit of order
(see
Fig. 1, where linear fit is used). Since we use a polynomial
fit of order 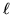 , we
denote the algorithm as DFA-
, we
denote the algorithm as DFA-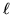 .
.
Figure 1:
(a) The correlated signal 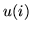 .
(b) The integrated signal:
.
(b) The integrated signal:
![$y(k)=\sum_{i=1}^k[u(i)-\langle u
\rangle]$](img78.png) . The vertical dotted lines indicate a box of size
. The vertical dotted lines indicate a box of size
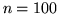 , the solid straight lines segments are the estimated
linear ``trend'' in each box by least-squares fit.
, the solid straight lines segments are the estimated
linear ``trend'' in each box by least-squares fit.
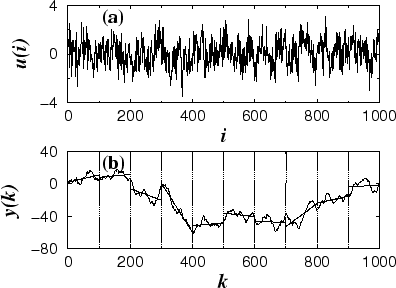 |
(iv) The integrated signal 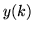 is detrended by
subtracting the local trend
is detrended by
subtracting the local trend 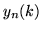 in each box of length
in each box of length  .
.
(v) For a given box size 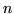 , the root mean-square (r.m.s.)
fluctuation for this integrated and detrended signal is
calculated:
, the root mean-square (r.m.s.)
fluctuation for this integrated and detrended signal is
calculated:
![\begin{displaymath}
F(n)\equiv\sqrt{{1\over {N_{max}}}\sum_{k=1}^{N_{max}}[y(k)-y_n(k)]^2}.
\end{displaymath}](img80.png) |
(3) |
(vi) The above computation is repeated for a broad range of scales
(box sizes 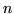 ) to provide a relationship between
) to provide a relationship between 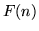 and the box
size
and the box
size 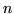 .
.
A power-law relation between the average root-mean-square
fluctuation function 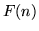 and the box size
and the box size 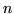 indicates
the presence of scaling:
indicates
the presence of scaling:
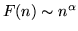 . The fluctuations can be
characterized by a scaling exponent
. The fluctuations can be
characterized by a scaling exponent 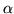 , a self-similarity
parameter which represents the long-range power-law
correlation properties of the signal. If
, a self-similarity
parameter which represents the long-range power-law
correlation properties of the signal. If 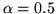 , there is no correlation
and the signal is uncorrelated (white noise); if
, there is no correlation
and the signal is uncorrelated (white noise); if
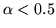 , the signal is anti-correlated; if
, the signal is anti-correlated; if
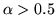 , the signal is correlated[64].
, the signal is correlated[64].
We note that for anti-correlated signals, the scaling exponent obtained
from the DFA method overestimates the true correlations at small scales[61].
To avoid this problem, one needs first to integrate the original anti-correlated
signal and then apply the DFA method[61]. The correct scaling
exponent can thus be obtained from the relation between 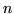 and
and 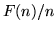 [instead of
[instead of 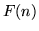 ].
In the following sections, we first integrate the signals under
consideration, then apply DFA-2 to remove linear trends in these
integrated signals. In order to provide a more accurate estimate of
].
In the following sections, we first integrate the signals under
consideration, then apply DFA-2 to remove linear trends in these
integrated signals. In order to provide a more accurate estimate of 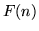 ,
the largest box size
,
the largest box size 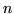 we use is
we use is 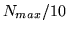 , where
, where 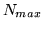 is the
total number of points in the signal.
is the
total number of points in the signal.
We compare the results of the DFA method obtained from the nonstationary
signals with those obtained from the stationary signal 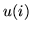 and examine
how the scaling properties of a detrended fluctuation function
and examine
how the scaling properties of a detrended fluctuation function 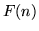 change
when introducing different types of nonstationarities.
change
when introducing different types of nonstationarities.


Next: Signals with segments removed
Up: Effect of nonstationarities on
Previous: Introduction
Zhi Chen
2002-08-28
![]() (
(
![]() ) with a standard
deviation
) with a standard
deviation ![]() . This method consists of the following steps:
. This method consists of the following steps:
![]() and calculate the Fourier transform coefficients
and calculate the Fourier transform coefficients ![]() .
.
![]() must exhibit correlations, which are
defined by the form of the power spectrum
must exhibit correlations, which are
defined by the form of the power spectrum

![]() is detrended by
subtracting the local trend
is detrended by
subtracting the local trend ![]() in each box of length
in each box of length ![]() .
.
![]() , the root mean-square (r.m.s.)
fluctuation for this integrated and detrended signal is
calculated:
, the root mean-square (r.m.s.)
fluctuation for this integrated and detrended signal is
calculated: