In this section, we study the effect of nonstationarity caused by removing
segments of a given length from a signal and stitching together the remaining
parts -- a ``cutting'' procedure often used in pre-processing data prior to
analysis. To address this question, we first generate a stationary correlated
signal ![]() (see Sec. 2) of length
(see Sec. 2) of length ![]() and a scaling exponent
and a scaling exponent ![]() , using the
modified Fourier filtering method[63]. Next, we divide this signal into
, using the
modified Fourier filtering method[63]. Next, we divide this signal into
![]() non-overlapping segments of size
non-overlapping segments of size ![]() and randomly remove
some of these segments. Finally, we stitch together the remaining segments in
the signal
and randomly remove
some of these segments. Finally, we stitch together the remaining segments in
the signal ![]() [Fig. 2(a)], thus obtaining a surrogate
nonstationary signal which is characterized by three parameters: the scaling
exponent
[Fig. 2(a)], thus obtaining a surrogate
nonstationary signal which is characterized by three parameters: the scaling
exponent ![]() , the segment size
, the segment size ![]() and the fraction of the signal
and the fraction of the signal
![]() , which is removed.
, which is removed.
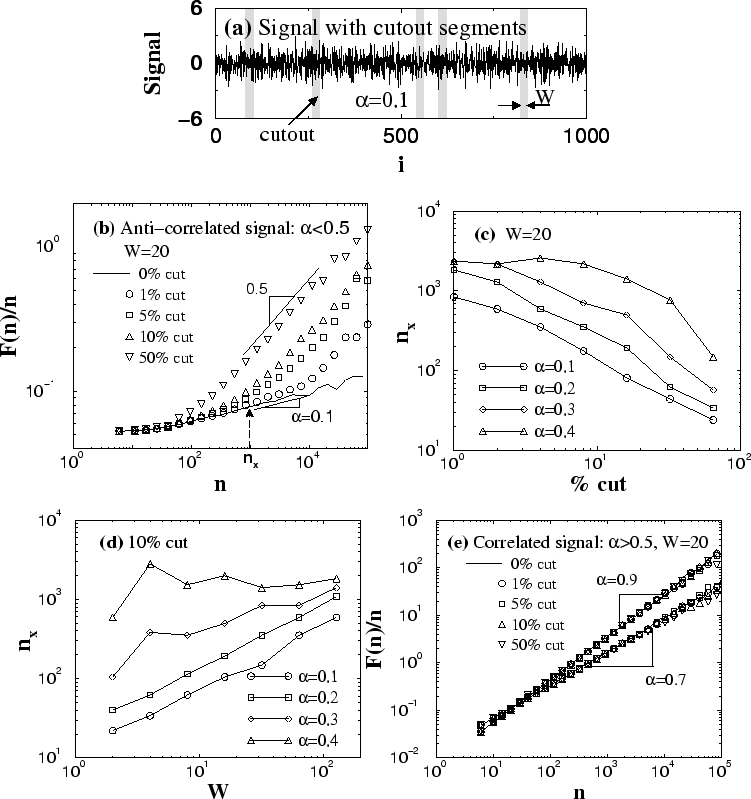 |
We find that the scaling behavior of such a nonstationary
signal strongly depends on the scaling exponent ![]() of the original
stationary correlated signal
of the original
stationary correlated signal ![]() . As illustrated in Fig. 2(b),
for a stationary anti-correlated signal with
. As illustrated in Fig. 2(b),
for a stationary anti-correlated signal with ![]() , the
cutting procedure
causes a crossover in the scaling behavior of the resultant nonstationary
signal. This crossover appears even when only
, the
cutting procedure
causes a crossover in the scaling behavior of the resultant nonstationary
signal. This crossover appears even when only ![]() of the
segments are cut out. At the scales larger than the crossover scale
of the
segments are cut out. At the scales larger than the crossover scale
![]() the r.m.s. fluctuation function behaves
as
the r.m.s. fluctuation function behaves
as
![]() , which means an uncorrelated randomness, i.e., the
anti-correlation has been completely destroyed in this regime. For all
anti-correlated signals with exponent
, which means an uncorrelated randomness, i.e., the
anti-correlation has been completely destroyed in this regime. For all
anti-correlated signals with exponent ![]() , we observe a
similar crossover behavior. This result is surprising, since researchers often
take for granted that a cutting procedure before analysis does not
change the scaling properties of the original signal. Our simulation shows that
this assumption is not true, at least for anti-correlated signals.
, we observe a
similar crossover behavior. This result is surprising, since researchers often
take for granted that a cutting procedure before analysis does not
change the scaling properties of the original signal. Our simulation shows that
this assumption is not true, at least for anti-correlated signals.
Next, we investigate how the two parameters -- the segment size ![]() and the
fraction of points cut out from the signal -- control the effect of the
cutting procedure on the scaling behavior of anti-correlated signals. For
the fixed size of the segments (
and the
fraction of points cut out from the signal -- control the effect of the
cutting procedure on the scaling behavior of anti-correlated signals. For
the fixed size of the segments (![]() ), we find that the crossover scale
), we find that the crossover scale
![]() decreases with increasing the fraction of the
cutout segments [Fig. 2(c)]. Furthermore, for anti-correlated
signals with small values of the scaling exponent
decreases with increasing the fraction of the
cutout segments [Fig. 2(c)]. Furthermore, for anti-correlated
signals with small values of the scaling exponent ![]() , e.g.,
, e.g.,
![]() and
and ![]() , we find that
, we find that ![]() and the fraction of
the cutout segments display an approximate power-law relationship. For a
fixed fraction of the removed segments, we find that the crossover scale
and the fraction of
the cutout segments display an approximate power-law relationship. For a
fixed fraction of the removed segments, we find that the crossover scale
![]() increases with increasing the segment size
increases with increasing the segment size ![]() [Fig. 2(d)]. To minimize the effect of the cutting procedure on the
correlation properties, it is advantageous to cut smaller number of segments
of larger size
[Fig. 2(d)]. To minimize the effect of the cutting procedure on the
correlation properties, it is advantageous to cut smaller number of segments
of larger size ![]() . Moreover, if the segments which need to be removed are
too close (e.g., at a distance shorter than the size of the segments), it
may be advantageous to cut out both the segments and a part of the signal
between them. This will effectively increase the size of the segment
. Moreover, if the segments which need to be removed are
too close (e.g., at a distance shorter than the size of the segments), it
may be advantageous to cut out both the segments and a part of the signal
between them. This will effectively increase the size of the segment ![]() without substantially changing the fraction of the signal which is cut out,
leading to an increase in the crossover scale
without substantially changing the fraction of the signal which is cut out,
leading to an increase in the crossover scale ![]() . Such strategy
would minimize the effect of this type of nonstationarity on the scaling
properties of data. For small values of the scaling exponent
. Such strategy
would minimize the effect of this type of nonstationarity on the scaling
properties of data. For small values of the scaling exponent ![]() (
(![]() ), we find that
), we find that ![]() and
and ![]() follow power-law
relationships [Fig. 2(d)]. The reason we do not observe a power-law
relationship between
follow power-law
relationships [Fig. 2(d)]. The reason we do not observe a power-law
relationship between ![]() and
and ![]() and between
and between ![]() and the
fraction of cutout segments for the values of the scaling exponent
and the
fraction of cutout segments for the values of the scaling exponent ![]() close to
close to ![]() may be due to the fact that the crossover regime becomes
broader when it separates scaling regions with similar exponents, thus
leading to uncertainty in defining
may be due to the fact that the crossover regime becomes
broader when it separates scaling regions with similar exponents, thus
leading to uncertainty in defining ![]() . For a fixed
. For a fixed ![]() and a fixed
fraction of the removed segments [see Figs. 2(c) and (d)], we
observe that
and a fixed
fraction of the removed segments [see Figs. 2(c) and (d)], we
observe that ![]() increases with the increasing value of the scaling
exponent
increases with the increasing value of the scaling
exponent ![]() , i.e., the effect of the cutting procedure on the scaling
behavior decreases when the anti-correlations in the signal are weaker
(
, i.e., the effect of the cutting procedure on the scaling
behavior decreases when the anti-correlations in the signal are weaker
(![]() closer to
closer to ![]() ).
).
Finally, we consider the case of correlated signals ![]() with
with
![]() . Surprisingly, we find that the scaling of correlated signals
is not affected by the cutting procedure. This observation remains true
independently of the segment size
. Surprisingly, we find that the scaling of correlated signals
is not affected by the cutting procedure. This observation remains true
independently of the segment size ![]() -- from very small
-- from very small ![]() up to very
large
up to very
large ![]() segments -- even when up to
segments -- even when up to ![]() of the segments are
removed from a signal with
of the segments are
removed from a signal with
![]() points [Fig. 2(e)].
points [Fig. 2(e)].