This description originally appeared in slightly modified form, and without the example, in Ho, Moody, Peng, et al. [4].
![]() is a ``regularity statistic'' that quantifies the unpredictability of
fluctuations in a time series such as an instantaneous heart rate time series,
is a ``regularity statistic'' that quantifies the unpredictability of
fluctuations in a time series such as an instantaneous heart rate time series,
![]() . Intuitively, one may reason that the presence of repetitive patterns
of fluctuation in a time series renders it more predictable than a time series
in which such patterns are absent.
. Intuitively, one may reason that the presence of repetitive patterns
of fluctuation in a time series renders it more predictable than a time series
in which such patterns are absent. ![]() reflects the likelihood that
``similar'' patterns of observations will not be followed by additional
``similar'' observations. A time series containing many repetitive patterns has
a relatively small
reflects the likelihood that
``similar'' patterns of observations will not be followed by additional
``similar'' observations. A time series containing many repetitive patterns has
a relatively small ![]() ; a less predictable (i.e., more complex) process has
a higher
; a less predictable (i.e., more complex) process has
a higher ![]() .
.
The algorithm for computing ![]() has been published elsewhere [1-4]. Here,
we provide a brief summary of the calculations, as applied to a time series of
heart rate measurements,
has been published elsewhere [1-4]. Here,
we provide a brief summary of the calculations, as applied to a time series of
heart rate measurements, ![]() . Given a sequence
. Given a sequence ![]() , consisting of
, consisting of ![]() instantaneous heart rate measurements
instantaneous heart rate measurements ![]() ,
, ![]() ,
, ![]() ,
, ![]() , we
must choose values for two input parameters,
, we
must choose values for two input parameters, ![]() and
and ![]() , to compute the
approximate entropy,
, to compute the
approximate entropy,
![]() , of the sequence. The second of these
parameters,
, of the sequence. The second of these
parameters, ![]() , specifies the pattern length, and the third,
, specifies the pattern length, and the third, ![]() , defines the
criterion of similarity. We denote a subsequence (or pattern) of
, defines the
criterion of similarity. We denote a subsequence (or pattern) of ![]() heart rate measurements, beginning at measurement
heart rate measurements, beginning at measurement ![]() within
within ![]() , by the
vector
, by the
vector ![]() . Two patterns,
. Two patterns, ![]() and
and ![]() , are similar if the
difference between any pair of corresponding measurements in the patterns is
less than
, are similar if the
difference between any pair of corresponding measurements in the patterns is
less than ![]() , i.e., if
, i.e., if
Now consider the set ![]() of all patterns of length
of all patterns of length ![]() [i.e.,
[i.e.,
![]() ], within
], within ![]() . We may now define
. We may now define
where ![]() is the number of patterns in
is the number of patterns in ![]() that are similar to
that are similar to
![]() (given the similarity criterion
(given the similarity criterion ![]() ). The quantity
). The quantity ![]() is the
fraction of patterns of length
is the
fraction of patterns of length ![]() that resemble the pattern of the same length
that begins at interval
that resemble the pattern of the same length
that begins at interval ![]() . We can calculate
. We can calculate ![]() for each pattern in
for each pattern in
![]() , and we define
, and we define ![]() as the mean of these
as the mean of these ![]() values. The
quantity
values. The
quantity ![]() expresses the prevalence of repetitive patterns of length
expresses the prevalence of repetitive patterns of length ![]() in
in ![]() . Finally, we define the approximate entropy of
. Finally, we define the approximate entropy of ![]() , for patterns of
length
, for patterns of
length ![]() and similarity criterion
and similarity criterion ![]() , as
, as
i.e., as the natural logarithm of the relative prevalence of repetitive
patterns of length ![]() compared with those of length
compared with those of length ![]() .
.
Thus, if we find similar patterns in a heart rate time series, ![]() estimates
the logarithmic likelihood that the next intervals after each of the patterns
will differ (i.e., that the similarity of the patterns is mere coincidence and
lacks predictive value). Smaller values of
estimates
the logarithmic likelihood that the next intervals after each of the patterns
will differ (i.e., that the similarity of the patterns is mere coincidence and
lacks predictive value). Smaller values of ![]() imply a greater likelihood
that similar patterns of measurements will be followed by additional similar
measurements. If the time series is highly irregular, the occurrence of similar
patterns will not be predictive for the following measurements, and
imply a greater likelihood
that similar patterns of measurements will be followed by additional similar
measurements. If the time series is highly irregular, the occurrence of similar
patterns will not be predictive for the following measurements, and ![]() will
be relatively large.
will
be relatively large.
It should be noted that ![]() has significant weaknesses, notably its strong dependence on
sequence length and its poor self-consistency (i.e., the observation that
has significant weaknesses, notably its strong dependence on
sequence length and its poor self-consistency (i.e., the observation that ![]() for one data set is larger than
for one data set is larger than ![]() for another for a given choice of
for another for a given choice of ![]() and
and ![]() should, but does not, hold true for other choices of
should, but does not, hold true for other choices of
![]() and
and ![]() ). For an excellent review of the shortcomings of
). For an excellent review of the shortcomings of ![]() and the strengths of alternative statistics, see reference [5].
and the strengths of alternative statistics, see reference [5].
Example:
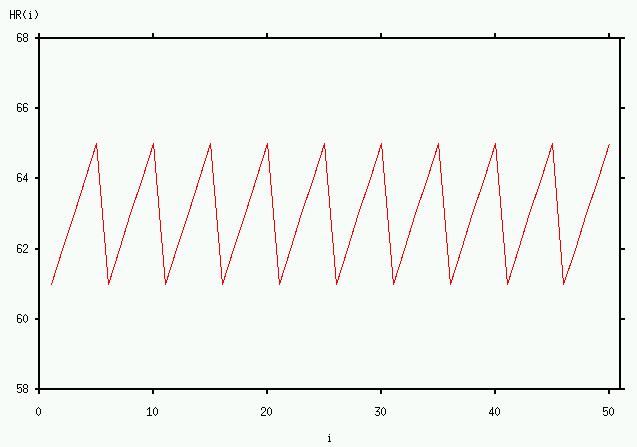
An example may help to clarify the process of calculating ![]() . Suppose that
. Suppose that
![]() , and that the sequence
, and that the sequence ![]() consists of 50 samples of the function illustrated above:
consists of 50 samples of the function illustrated above:
(i.e., the sequence is periodic with a period of 5). Let's choose ![]() (this choice simplifies the calculations for this example, but similar results
would be obtained for other nearby values of
(this choice simplifies the calculations for this example, but similar results
would be obtained for other nearby values of ![]() ) and
) and ![]() (again, the
value of
(again, the
value of ![]() can be varied somewhat without affecting the result). This gives
us:
can be varied somewhat without affecting the result). This gives
us:

and so on. The first question to be answered is: how many of the ![]() are similar to
are similar to ![]() ? Since we have chosen
? Since we have chosen ![]() as the similarity
criterion, this means that each of the 5 components of
as the similarity
criterion, this means that each of the 5 components of ![]() must be within
must be within
![]() units of the corresponding component of
units of the corresponding component of ![]() . Thus, for example,
. Thus, for example,
![]() is not similar to
is not similar to ![]() , since their last components (61 and 65)
differ by more than 2 units. The conditions for similarity to
, since their last components (61 and 65)
differ by more than 2 units. The conditions for similarity to ![]() will
be satisfied only by
will
be satisfied only by ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ...,
, ...,
![]() , as well as by
, as well as by ![]() itself [i.e., for 10 of the
itself [i.e., for 10 of the ![]() ], so we
have
], so we
have
Since the total number of ![]() is
is
![]() ,
,
We can now repeat the above steps to determine how many of the ![]() are
similar to
are
similar to ![]() ,
, ![]() , etc.
By the same reasoning,
, etc.
By the same reasoning, ![]() is similar to
is similar to ![]() ,
, ![]() ,
, ![]() ,
...,
,
..., ![]() , so that
, so that
and in general
(This last statement is true only for the particular example we are considering, since we have specified a sequence with a period of 5, and we have chosen m = 5 as well.)
Hence ![]() is either
is either ![]() or
or ![]() , depending
on
, depending
on ![]() , and the mean value of all 46 of the
, and the mean value of all 46 of the ![]() is:
is:
In order to obtain ![]() , we need to repeat all of the calculations
above for
, we need to repeat all of the calculations
above for ![]() . Doing so, we obtain:
. Doing so, we obtain:
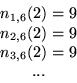
so that
and ![]() . Finally, we calculate that
. Finally, we calculate that
This is a very small value of ApEn, which suggests that the original time series is highly predictable (as indeed it is).
ApEn Software
In view of the weaknesses in ApEn, and in deference to the wishes of SM Pincus, we do not provide an implementation of ApEn here. This description is provided here so that researchers who wish to use ApEn can write their own code for doing so.
An ApEn implementation in Matlab m-code is included in Danny Kaplan's Software for Heart Rate Variability.
References:
1. Pincus SM. Approximate entropy as a measure of system complexity. Proc Natl Acad Sci USA 1991;88:2297-2301.
2. Pincus SM, Goldberger AL. Physiological time-series analysis: What does regularity quantify? Am J Physiol 1994;266(Heart Circ Physiol):H1643-H1656.
3. Ryan SM, Goldberger AL, Pincus SM, Mietus J, Lipsitz LA. Gender and age-related differences in heart rate dynamics: Are women more complex than men? J Am Coll Cardiol 1994;24:1700-1707.
4. Ho KKL, Moody GB, Peng CK, Mietus JE, Larson MG, Levy D, Goldberger AL. Predicting survival in heart failure case and control subjects by use of fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics. Circulation 1997 (August);96(3):842-848.
5. Richman JS, Moorman JR. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol 278(6):H2039-H2049 (2000).
|
If you would like help understanding, using, or downloading content, please see our Frequently Asked Questions. If you have any comments, feedback, or particular questions regarding this page, please send them to the webmaster. Comments and issues can also be raised on PhysioNet's GitHub page. Updated Thursday, 9 July 2015 at 11:08 EDT |
PhysioNet is supported by the National Institute of General Medical Sciences (NIGMS) and the National Institute of Biomedical Imaging and Bioengineering (NIBIB) under NIH grant number 2R01GM104987-09.
|